Второй постулат Евклида формулируется следующим образом: «2. И что ограниченную прямую <можно> продолжать по прямой» [1, с. 14]. Многие ученые считают этот постулат «интуитивно очевидным». Действительно, имея прямую AB, надо взять линейку достаточной длины и, совместив край линейки с точками A и B, отметить на продолжении линейки точку C (рис. 1).

Рис. 1
Затем, сдвинув линейку и совместив её край с точками B и C, провести прямую BC и отметить на продолжении линейки точку D (рис. 2).

Рис. 2
Повторяя эту процедуру, прямую AB можно сколь угодно продолжать.
Вот только в своих «Началах» Евклид ни разу не использовал понятие линейка и допускал только возможность того, что: «1. Что от всякой точки до всякой точки <можно> провести прямую линию» [1, с. 14].
Предположим, что задана прямая AB. Возьмем произвольную точку D, лежащую вне прямой AB (проекция этой точки не находится на ней) (рис. 3).
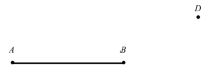
Рис. 3
Теперь через точку D проведем две окружности (третий постулат): одну окружность a с центром в точке A, другую – b с центром в точке B. «Тогда эти окружности имеют две и только две точки пересечения» (D и E) [2, с. 47] (рис. 4).
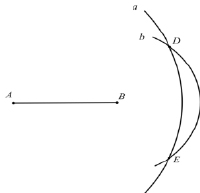
Рис. 4
Далее, проведем прямую DE и найдем точку C, соответствующую середине этой прямой (предложение 10 книги первой) (рис. 5).
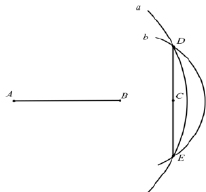
Рис. 5
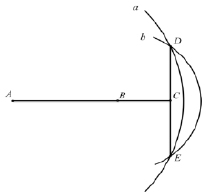
Рис. 6
Теперь проведем прямые AC и BC (рис. 6).
Эти прямые являются перпендикулярными к прямой DE (предложение 12 книги первой). Учитывая, что прямые AC и BC имеют общую точку C на прямой DE, и тот факт, что перпендикулярная прямая к заданной прямой определяется единственным образом [3], приходим к выводу: прямая BC является частью прямой AC. Следовательно, точка C лежит на продолжении прямой AB. Таким образом, прямую можно продолжать неограниченно.
Библиографическая ссылка
Черкасов М.Ю. ДОКАЗАТЕЛЬСТВО ВТОРОГО ПОСТУЛАТА ЕВКЛИДА // Научное обозрение. Реферативный журнал. 2017. № 1. С. 85-86;URL: https://abstract.science-review.ru/ru/article/view?id=1853 (дата обращения: 29.01.2026).
 science-review.ru
science-review.ru