Эксплуатация реальных конструкций может происходить в самых разнообразных условиях и средах, зачастую в той или иной мере агрессивных по отношению к материалу конструкции. Эти среды могут быть природными, техногенными или смешанными. Отдельные агрессивные компоненты этих сред могут диффундировать в объем материала и вступать в физическое и/или химическое взаимодействие с ним. Это взаимодействие может приводить к изменению служебных свойств материала и конструкции в целом. Агрессивная среда оказывает значительное влияние на механические, физические, химические, электротехнические и другие характеристики материала.
Воздействие агрессивной среды на металл определяется также видом ее агрегатного состояния – это может быть жидкая среда, газообразная среда и плазма. Примером жидкой среды может служить жидкометаллический теплоноситель в контуре водо-водяного энергетического реактора, его воздействие может вызывать коррозионное растрескивание материала элементов оборудования атомных электростанций (АЭС). При высоких температурах агрессивный характер имеет даже обычная воздушная среда, вызывающая в этом случае высокотемпературную газовую коррозию. Ионизирующее излучение также можно считать агрессивной средой, так как радиационные эффекты влияют на кристаллическую решетку металлов и в результате происходит распухание металла, а влияние ионизирующего излучения на полимеры характеризуется изменением их структурных элементов.
Предлагаемый обзор научных исследований посвящен анализу существующих подходов, методов и решений в этой важной области прочности материалов и конструкций, контактирующих со средой. Эти исследования имеют как фундаментальное, так и широкое прикладное значение для проектирования элементов конструкций, подверженных влиянию агрессивной рабочей среды и окружающей внешней среды, которая при определенных условиях может быть агрессивной. Первостепенность фундаментального подхода связана с построением механико-математических моделей, основанных на определяющих и кинетических уравнениях и описывающих процессы деформирования и разрушения конструкций и процессы взаимодействия материала и конструкций с указанными средами. Идентификация этих моделей, то есть определение значений коэффициентов (материальных параметров) в этих уравнениях и подбор подходящих материальных функций основываются на обработке экспериментальных данных, в результате решения полученной совокупности уравнений проводится анализ поведения конструкций в различных условиях.
В настоящем обзоре особенное влияние уделяется именно влиянию агрессивной среды на высокотемпературную кратковременную и длительную прочность материалов и элементов конструкций. А это в свою очередь существенно влияет на длительную работоспособность конструкций в целом и безопасность их эксплуатации в течение всего срока службы. Степень важность безопасной эксплуатации конструкций, ответственных конструкций, в том числе применяемых в нефтехимическом машиностроении и атомной энергетике не подлежит сомнению, а нарушения в этих областях могут приводить к техногенным авариям, и как следствие возможным экологическим катастрофам. Поэтому технологии предупреждения и ликвидации чрезвычайных ситуаций природного и техногенного характера входят в перечень критических технологий и приоритетных направлений развития науки, техники и технологий, утвержденных Президентом Российской Федерации [103].
Взаимодействие физических и химических процессов в металлах
Теоретические разработки влияния агрессивной среды на материал рекомендуется начинать с изучения и анализа физико-химических аспектов такого взаимодействия. Ряд известных монографий посвящен такому изучению и анализу. Среди них можно отметить работы А.Н. Фрумкина с соавторами [112], Ю.Р. Эванса [117], Э.М. Гутмана [11], Н. Биркса и Дж. Майера [6], A. Веста [7, 8], Г.Г. Улига и Р.У. Реви [104], И.В. Семеновой с соавторами [99] и др. Кроме того, некоторые данные по физике твердого тела, химическим процессам, коррозионным взаимодействиям можно получить из энциклопедий и справочников (см., например, [22, 105, 113]). Исследования этих авторов основываются на глубоком атомно-молекулярном изучении физико-химических процессов в материале при воздействии на него активной среды, в частности, учете ионных потоков (анионно-катионных процессов) и движения электронов, участвующих в коррозионных процессах. В результате детального исследования авторы осуществляют построение физико-химических моделей, которые связывают основные термодинамические и физико-химические параметры изучаемых процессов на более высоком, по сравнению с атомно-молекулярным, уровне. Таким образом, как результат, указанные модели устанавливают зависимость между параметрами окружающей среды (температурой, влажностью, химическим составом среды, продолжительностью воздействия и т.д.) и параметрами коррозионного процесса. Однако, как отмечают в своей монографии И.Г. Овчинников и Г.А. Наумова [74], особенностью физико-химических моделей является их строгая индивидуальность. При переходе к конструкциям из других сталей, с другими формами и размерами поперечных сечений, находящимися в других районах с другими параметрами внешней среды, с другими защитными покрытиями, используемые модели могут дать существенно отличающиеся результаты.
Физико-химические модели процессов взаимодействия агрессивной среды с материалами позволяют в дальнейшем перейти к построению механико-математических (феноменологических) и структурных моделей. Эти модели позволяют прогнозировать рассматриваемые явления и в дальнейшем учитывать их влияние на макромеханическое поведение материалов и элементов конструкций под действием нагрузок с учетом агрессивного воздействия среды.
Феноменологический подход при моделировании процессов взаимодействия среды с материалами и элементами конструкций
Для того, чтобы перейти к построению механико-математических (феноменологических) моделей, необходимо выбрать феноменологические параметры, изменение которых можно было бы наблюдать во время эксперимента, или структурные параметры – так называемые кинетические параметры процесса взаимодействия материала и проникающей в него среды. Введение кинетических параметров в модели позволяет провести описание реальных экспериментальных данных с помощью рассматриваемой математической модели при различных программах температурно-силового нагружения. К феноменологическим параметрам можно относить толщину слоя δ материала, который уже подвергнут деструктивному влиянию среды (например, коррозионный износ), а к кинетическим параметрам – также, по мнению некоторых авторов, относят толщину слоя δ, параметр коррозионной поврежденности ω, концентрацию элементов агрессивной среды c в металле и др.
Работы, учитывающие толщину коррозионного слоя δ
К «пионерским» работам, в которых исследуется коррозионный износ, можно отнести работы А.И. Кикина [20] и В.М. Долинского [15]. В 1967 г. В.М. Долинский в своих научных работах использует «механохимическую» модель коррозионного износа, в которой используется зависимость скорости коррозии от уровня механического растягивающего напряжения. В частности, автор [15] предлагает решение задачи прочностного расчета тонкостенной оболочки, подвергающейся сплошной коррозии, скорость которой считается функцией интенсивности напряжений. Далее такой подход В.М. Долинский [16] распространил на прочностной анализ оболочек, трубчатых аппаратов и круглых пластин, используемых в нефтехимии и энергетике. В этих работах показано, что неравномерность поля напряжений приводит к неравномерному коррозионному износу.
В этом разделе статьи рассматриваются виды моделей коррозионного износа и конкретные соотношения, которые не учитывают природу взаимодействия агрессивной среды с материалом конструкции. Здесь не имеет значения, происходит ли физическое проникновение агрессивного вещества в сплошную среду, или это проникновение сопровождается химическим взаимодействием и превращениями. Значения материальных параметров в феноменологических моделях определяются на основе обработки конкретных экспериментальных данных.
Для параметра δ предложено много различных моделей. Так, в монографии И.Г. Овчинникова и Г.А. Наумовой [74] приведены примеры таких математических моделей, все коэффициенты, используемые в этих моделях, безусловно неявно зависят от компонентов тензора напряжений δij. Дополнительно авторы группируют механико-математические модели, в которых явно учитывается влияние напряженного состояния δij на кинетику коррозионного износа элементов конструкций. В приведенных в [74] зависимостях δ = δ(t) все входящие величины, кроме δ, времени t, температуры T и характеристик напряженно-деформированного состояния представляют собой материальные функции и коэффициенты, определяемые по экспериментальным данным.
Указанные механико-математические модели имеют универсальный характер, они приемлемы для научных и инженерных расчетов прогноза изменения характерных размеров элементов конструкций, а, следовательно, и несущей способности и поведения конструкции при воздействии на нее факторов агрессивной окружающей и/или рабочей сред.
В [60] проводится систематизация различных моделей взаимодействия материалов с агрессивной средой. В [70, 73] указывается целесообразность использования банков моделей, учитывающих явление коррозии. В предлагаемом банке содержится информация о видах моделей, значениях коэффициентов для разных условий, областях применения моделей. Кроме того, в [70, 73] приведены рекомендации по работе с разными моделями, данные о конструкциях, рассчитанных с использованием моделей, и библиография работ, в которых встречаются конкретные модели.
В конце 1970-х и начале 1980-х годов Э.М. Гутман с соавторами [11, 12, 13, 14] исследовали долговечность сосудов высокого давления в условиях механохимической коррозии (скорость коррозии зависит от напряженного состояния) при упругопластических деформациях. Кроме того, эти авторы проводили экспериментальное и теоретическое исследование напряженно-деформированного состояния пластин в условиях чистого изгиба в коррозионной среде и определяли прочность газопромысловых труб в условиях коррозионного износа. В этих работах предполагается, что скорость коррозии экспоненциально зависит от среднего напряжения, что мнению И.Г. Овчинникова не всегда справедливо [58]. Следует отметить работы В.Г. Карпунина с соавторами [18, 19], в которых учитывается различие скоростей коррозии на разных изгибаемых поверхностях пластин и оболочек. Так, при уменьшении толщины пластин вследствие коррозионного износа, прогибы и углы поворота могут стать большими, а напряжения могут превысить предел текучести материала. В этих работах получены уравнения, описывающие процесс коррозионного разрушения гибких прямоугольных пластин и пологих оболочек из упругопластического материала с учетом несимметричности толщины относительно поверхности приведения. Учет физической и геометрической нелинейности в ряде случаев приводит к значительному изменению характера напряженно-деформированного состояния и, следовательно, уточняет процесс описания деформирования и разрушения пластин и оболочек.
Большой вклад в развитие прочностного расчета пластин, оболочек, толстостенных труб и других элементов конструкций, подверженных коррозионному износу, внесла Саратовская школа механиков под руководством И.Г. Овчинникова и В.В. Петрова.
И.Г. Овчинников с соавторами разработали методологию построения и исследования расчетных моделей конструкций, подвергающихся деструктирующему воздействию агрессивных сред, построили ряд моделей конструкций, подвергающихся коррозионному износу, воздействию водорода высоких и низких параметров, радиационному облучению, воздействию жидкометаллических сред. В [71] ими предложена логистическая модель коррозионного износа, основанная на логистическом уравнении:
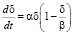 ,
, 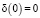 ,
,
где α, β – параметры. В [61] И.Г. Овчинников предложил энергетическую модель коррозионного разрушения, инвариантную к виду напряженного состояния. Эта инвариантная особенность модели позволяет идентифицировать ее параметры в одних условиях, а использовать в других условиях деформирования материала.
В работах Ю.Г. Прониной [87, 88, 98, 124] рассматриваются задачи механохимической коррозии, в которых задаются соотношения для dδ/dt для наружных и внутренних радиусов толстостенных труб и полых сфер во времени в виде эмпирических зависимостей от напряжения и температуры. В этих работах учитывается возможность затухания коррозии во времени при образовании плотной пленки окислов (например, по экспоненциальному закону). Полученные изменения толщин учитываются при решении задачи Ламе. Для оценки долговечности дополнительно учитывается накопление повреждений, определяемых как отношение текущего максимального главного напряжения к пределу прочности.
Во многих работах наряду с параметром δ используется параметр коррозионной поврежденности ω. Значение параметра коррозионной поврежденности ω изменяется от ω = 0 в начальный момент времени до ω = ω* в момент разрушения (обычно в качестве величины ω* принимается значение 1). В общем случае кинетическое уравнение для параметра ω имеет следующий вид:
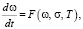 (1)
(1)
где t – время, σ – напряжение, T – температура.
Уравнение (1) используется во многих работах И.Г. Овчинникова с соавторами [10, 57, 64, 66 – 69], посвященных исследованию ползучести и длительной прочности элементов конструкций с учетом влияния агрессивной среды. Так, в [10, 66] исследуется поведение прямоугольных пластинок, подвергающихся высокотемпературному окислению в условиях ползучести. В [57, 64] определяется длительная прочность пластинок и оболочек в условиях коррозионного износа. В [67 – 69] выводятся основные соотношения, описывающие ползучесть и длительную прочность пластинки, подвергающейся окислению. Здесь подробно исследуются закономерности окисления и способы его описания, идентификация некоторых моделей, описывающих кинетику окисления, основные соотношения, описывающие ползучесть и длительную прочность пластинки, подвергающейся окислению, алгоритм расчета ползучести пластинки, подвергающейся окислению. Рассматриваются различные феноменологические модели изменения толщины окисленного слоя δ(t) и кинетические соотношения для накопления коррозионных повреждений, имеющие имеет вид (1). Коэффициенты в этих моделях определяются на основе обработки экспериментальных данных. Накопление повреждений учитывается в основных соотношениях ползучести и длительной прочности, а изменение толщины пластины учитывается в постановке задачи. Дополнительно исследуется влияние различных факторов, в том числе влияние вида нагрузки и закрепления, на кинетику накопления повреждений и коррозионный износ прямоугольной пластинки. Расчет конструкций с учетом совместного действия нагрузок, температур и коррозионного износа предлагается в работах [65, 67, 68, 69, 79].
На протяжении 25 лет в Научно-исследовательском Институте механики МГУ имени М.В. Ломоносова под руководством А.М. Локощенко проводятся систематические исследования влияния агрессивной среды на ползучесть и длительную прочность металлов. Это исследование основано на применении кинетической концепции Ю.Н. Работнова [92]. Анализ проводится с помощью введения двух зависящих от времени и пространственных координат параметров: один из них – поврежденность материала, в качестве второго параметра принимаются толщина разрушенного поверхностного слоя или концентрация специфических характеристик окружающей среды в металле. Результаты этих исследований приведены в монографиях А.М. Локощенко [34, 36, 37].
В 1995 – 1997 гг. А.М. Локощенко проанализировал известные экспериментальные данные по длительной прочности образцов с различными значениями поперечных размеров и обнаружил значительный масштабный эффект, проявляющийся в том, что образцам большей толщины соответствует большее значение времени до разрушения при одной и той же величине растягивающего напряжения. Этот эффект А.М. Локощенко описал на основе изучения коррозии металлов, характеризуемой разрушением поверхностного слоя металлов, возникающего на всех боковых поверхностях испытываемых образцов [29 – 31]. Им был предложен метод оценки влияния поперечных размеров образцов на длительную прочность, который основан на учете различной роли поверхностных и внутренних слоев металла в реальных испытаниях. Были введены понятия «сильного» и «слабого» масштабных эффектов. Предложены различные варианты систем кинетических уравнений относительно поврежденности материала и толщины разрушенного слоя, позволяющие качественно и количественно описывать различные особенности проявления масштабного эффекта.
Работы, учитывающие диффузионное проникновение агрессивной среды в материал
Как известно, математические модели физических явлений описываются с помощью уравнений математической физики [102], как правило, это дифференциальные уравнения в частных производных. Так, например, процесс физической диффузии по типу Фика описывается параболическим уравнением в частных производных [102]:
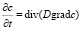 , (2)
, (2)
где c – концентрация среды в материале, t – время, D – коэффициент диффузии.
Точные решения уравнения диффузии для тел с постоянными границами представляются обычно в виде тригонометрических рядов или рядов, состоящих из специальных функций, которые не всегда позволяют получить представление искомых характеристик в обозримом анализируемом виде. Эти решения громоздки по виду, и для получения приемлемой точности в расчетах необходимо удерживать большое количество членов ряда. В связи с этим целесообразно использовать приближенные решения уравнений диффузии.
А.М. Локощенко с учениками используют приближенный метод решения уравнения диффузии, основанный на введении диффузионного фронта агрессивной среды в материале [34, 36, 37, 43, 45 – 48]. Основа этого подхода заключается во введении диффузионного фронта, разделяющего невозмущенную и возмущенную области рассматриваемого тела, и определении движения границы между этими областями. Показаны высокая точность и эффективность предлагаемого метода. Этот метод позволяет представить решение уравнения диффузии в удобной для анализа форме. Получена система уравнений, описывающих взаимодействие диффузионного и коррозионного фронтов в процессе ползучести. Приведены решения типовых задач при различных граничных условиях. Предложен упрощенный вариант данного метода, в котором накопление поврежденности материала во времени зависит от интегрально среднего (в объеме тела) значения концентрации элементов окружающей среды в металле. Предложен критерий длительной прочности, связывающий времена разрушения в присутствии и отсутствии агрессивной окружающей среды. В [42] приведено описание так называемого запирающего эффекта, при котором плотный слой проникших посредством диффузии элементов среды приводит к практическому прекращению диффузионного процесса.
А.М. Локощенко и Л.В. Фомин применили этот метод при решении задач растяжения, изгиба, нестационарного сложного напряженного состояния стержней и пластин при ползучести с учетом влияния агрессивной среды [39, 45 – 48, 107, 108]. Наряду с наиболее распространенной степенной зависимостью скорости деформации ползучести и скорости накопления поврежденности от напряжения, в этих работах также используется дробно-степенная модель ползучести и длительной прочности, предложенная ранее С.А.zШестериковым и М.А. Юмашевой [116].
А.М. Локощенко, А.А. Ильин, А.М. Мамонов и В.В. Назаров [32, 40, 41, 44] провели экспериментально-теоретическое исследование ползучести и длительной прочности двухфазного титанового сплава ВТ6 с предварительно внедренным водородом. Были проведены испытания растягиваемых образцов на ползучесть вплоть до разрушения в широком диапазоне значений напряжений и уровней концентрации водорода. Испытания показали, что увеличение доли предварительно внедренного водорода приводит к систематическому уменьшению скорости ползучести, увеличению времени до разрушения и, как правило, к уменьшению предельной деформации в несколько раз. С помощью кинетического подхода получено хорошее соответствие экспериментальных и теоретических кривых ползучести вплоть до разрушения. Исследование структуры исходных и испытанных образцов показало, что предварительное внедрение водорода в двухфазный сплав ВТ6 приводит к значительному перераспределению долей α- и β-фаз в сплаве, именно это обстоятельство является причиной изменения механических характеристик сплава вследствие внедрения водорода.
В.И. Астафьев и Л.К. Ширяева [3, 4] на основе обобщенного подхода Ю.Н. Работнова – Л.М. Качанова предложили математическую модель упругопластического деформирования металлов в агрессивных средах, которое приводит к потере пластичности и охрупчиванию металлов. Предложенные определяющее и кинетическое соотношения позволили описать ряд общих закономерностей растрескивания под напряжением и водородного охрупчивания. В [3, 4] исследована зависимость этих закономерностей от скорости деформирования, величины содержания водорода и вида напряженного состояния.
А.М. Локощенко и Д.А. Кулагин [26, 27, 42, 122, 123] предложили теорию ползучести и длительной прочности, которая основана на вероятностном подходе. Предложено подробное описание данной модели при рассмотрении длительной прочности растягиваемого стержня с поперечным сечением в виде узкого прямоугольника. Принимается, что стержень состоит из большого количества плотно уложенных очень тонких пластин. Принята гипотеза о вероятности разрушения этих пластин, которая зависит от осевого напряжения и концентрации в материале стержня элементов окружающей среды. Эта гипотеза приводит к тому, что с течением времени отдельные пластины разрушаются, причем плотность неразрушенных пластин возрастает по направлению от боковой поверхности стержня к его середине. Это обстоятельство приводит к появлению неоднородного поля осевых напряжений (с максимумом вдоль оси стержня). Уменьшение количества неразрушенных пластин приводит к увеличению напряжения в каждой пластине и в итоге – к полному разрушению стержня. Рассмотрены возможности вероятностного подхода при рассмотрении стержня при чистом изгибе, толстостенной трубы под внутренним давлением цилиндрической оболочки при двухосном растяжении и др. В [35] рассмотрена длительная прочность растягиваемого цилиндрического стержня с помощью вероятностной модели.
И.Г. Овчинников [62] предложил диффузионную модель коррозионного разрушения (с применением параметра коррозионной поврежденности ω), которая экспериментально обоснована в статье [56].
Работы, учитывающие химическое взаимодействие агрессивной среды с материалом
В.В Петров, И.Г Овчинников и В.К. Иноземцев в монографии [85], кроме концентрации c и поврежденности ω, дополнительно рассматривают кинетический параметр химического взаимодействия q, изменяющийся от 0 (перед началом химической реакции) до 1 (в конце реакции) и определяемый кинетическим уравнением
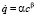 . (3)
. (3)
В этом случае входящие в кинетическое уравнение для поврежденности
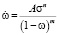 (4)
(4)
величины A, n, m зависят от q.
В ряде случаев рекомендуется для более точного описания экспериментальных данных использовать вместо уравнения (3) уравнение
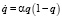 . (5)
. (5)
И.Г. Овчинников и В.В. Петров [76] сравнивают характерные скорости процессов диффузии Vдифф. и химической реакции Vхим., анализируют последствия существенного различия этих скоростей и предлагают вводить движущийся фронт изменения механических характеристик. Параметр химического взаимодействия q и разделение областей материала (в данном случае полимера) на различные кинетические области в зависимости от соотношения скорости диффузии Vдифф. и скорости химического взаимодействия Vхим. рассматриваются И.Г. Овчинниковым также в статье [63]. В зависимости от упомянутых факторов, в [63] отдельно рассматриваются три такие области, в которых происходят деструкция материала и выполняется одно из трех неравенств: Vхим. >> Vдифф., Vдифф. >> Vхим. или Vдифф. ≈ Vхим..
В [72, 80] для анализа влияния водородной коррозии на механические свойства вместо ω(t) вводится интегральный параметр q(t) химического взаимодействия металла с водородной средой. Все коэффициенты, входящие в определяющие уравнения, заменяются на функции q(t). Под q(t) понимается кусочно-постоянная функция времени t, зависящая от двух времен: продолжительности инкубационного периода (в течение которого механические свойства материала не меняются) и времени до завершения химических превращений в материале.
При учете химического взаимодействия агрессивной среды с материалом логично было бы модифицировать указанное параболическое уравнение диффузии (2), вводя в него дополнительные слагаемые, учитывающие дополнительные источники или стоки проникающего в материал вещества, которые возникают при химических превращениях и поглощениях вещества в процессе химических реакций. Также в качестве таких дополнительных слагаемых могут вводиться скорости этих потоков, т.е. скорости изменения концентрации во времени. Одна из известных работ в этом научном направлении написана британским ученым J. Crank-ом [119]. Эта монография посвящена описанию диффузионных процессов в терминах решений дифференциальных уравнений. В разделе этой книги, который имеет название «Diffusion and chemical reaction», автор приводит различные модификации уравнения диффузии, естественное обоснование их получения (на основе физических и химических принципов, балансов веществ) и методы решения таких модифицированных уравнений. Кроме этой книги, авторам настоящего отчета неизвестны подобные исследования в этом научном направлении.
В статье [76] И.Г. Овчинников и В.В. Петров подробно рассматривают взаимодействие физико-химических процессов с помощью параметров с и q, используя систему уравнений, состоящую из уравнений и модифицированного уравнения диффузии:
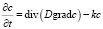 , (6)
, (6)
где k = const – характерная скорость химической реакции, kc – скорость распада химических связей под действием агрессивной химической среды.
В [77] И.Г. Овчинников и А.Б. Рассада исследовали деформирование сплошной среды, взаимодействующей с водородосодержащей средой, модифицированное уравнение диффузии в этом случае учитывает градиент напряжений в сплошной среде (D = const)
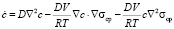 . (7)
. (7)
Здесь c – концентрация молекулярного водорода, V – мольный объем, R – газовая постоянная, σcp – среднее нормальное напряжение. Компоненты тензоров напряжений и деформаций связаны соотношениями, коэффициенты которых зависят от c и характеристики вида напряженного состояния 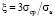 , σu – интенсивность напряжений.
, σu – интенсивность напряжений.
Существенные результаты в исследовании влияния агрессивной среды, вступающей как в физическое, так и в химическое взаимодействие с материалом с учетом фазовых превращений, получены Фрейдиным А.Б. в течение последних 30 лет. Среди работ автора, опубликованных в течение последних пяти лет, можно отметить следующие работы: [9, 21, 109 – 111].
В этих работах автора рассматривается развитие механико-математических моделей для описания влияния механических напряжений на кинетику химических реакций в деформируемых телах. При этом учитывается физико-химическое обоснование описываемых подходов, в частности, используются уравнения химических реакций, которые происходят на границах раздела твердых фаз (металл, оксид) и газообразных веществ. Модели учитывают влияние как внешних, так и порождаемых химическими реакциями внутренних напряжений. Исследуется влияние вида напряженного состояния, величин и знаков напряжений на протекание химических реакций. Исследуется устойчивость распространения фронта химической реакции в напряженном теле. Рассматриваются кинетика фронта реакции в окрестности концентраторов напряжений и взаимосвязи химических реакций с процессами разрушения. С учетом химической реакции, локализованной на фронте реакции в открытой системе «деформируемое тело – газообразная компонента», записывается баланс массы, импульса и энергии, после чего выводится выражение для производства энтропии, позволяющее естественным образом получить формулу для тензора химического сродства, с помощью которого определяются как химическое равновесие, так и кинетика фронта превращения. Обсуждается также запирающий эффект – блокирование реакции напряжениями на фронте. Проводится сравнение условий на межфазной границе и на фронте химической реакции. Формулируется задача о деформируемом твердом теле с неизвестной внутренней границей, положение которой в случае термодинамического равновесия согласно принципу Гиббса минимизирует энергию тела. В работах А.Б. Фрейдина показано, что на термодинамически равновесной границе равенство скалярных химических потенциалов заменяется равенством нормальных компонент тензора химического потенциала, в роли которого выступает тензор напряжений Эшелби, поделенный на плотность материала в отсчетной конфигурации [118, 120, 121].
На протяжении последних шестидесяти лет в Физико-механическом институте имени Г.В. Карпенко НАН Украины ведется плодотворное исследование влияния окружающей среды на характеристики металлов при высоких температурах (Г.Г. Максимович, Н.П. Дрозд, В.Н. Федирко, В.С. Павлина, Я.С. Матычак и др.). Основная особенность теоретических работ этой группы ученых заключается в исследовании взаимосвязи деформационных процессов с адсорбцией, диффузией, химическими реакциями, теплопроводностью и т.д. Ученые проводят анализ взаимодействия процессов диффузионного насыщения и протекания внутренней химической реакции, с этой целью они рассматривают систему уравнений диффузии с дополнительными членами и с помощью метода Лапласа получают ее решение. Это решение позволяет исследовать стадию однородного образования химических комплексов и выявить их влияние на кинетику перераспределения диффундирующих элементов. В работе [83] предложенный метод распространен на дополнительное описание сублимации легирующих элементов с одновременным распадом химических соединений в сплавах.
Отдельный интерес представляет исследование влияния ионизирующего излучения на деформационно-прочностные характеристики материалов и элементов конструкций. Как отмечалось во введении, ионизирующее излучение также можно считать агрессивной средой, влияющей на физико-механические характеристики материала, подвергнутого ее влиянию. Это влияние заключается в появлении радиационных дефектов кристаллической решетки металлов и распухании металла (увеличение объема металла при воздействии на него ионизирующего излучения). В статье И.И. Овчинникова, И.Г. Овчинникова и М.Ю. Богина, [75] рассматриваются особенности методологии построения моделей деформирования и разрушения материалов в условиях радиационного облучения с использованием теории кинетических параметров Ю.Н. Работнова [92]. Приводятся модели, описывающие изменение дозы облучения (флюенса) нейтронного потока по объему конструктивного элемента, а также модели, описывающие радиационные деформации (распухание) материала. Анализируются результаты экспериментов по влиянию типа и вида напряженного состояния на радиационное распухание и ползучесть материалов.
Во всех ранее рассмотренных работах использовался детерминированный подход с изучением влияния среды и расчетов элементов конструкций, подверженных этому влиянию. В случае случайного характера коррозионного процесса значительный интерес представляет вероятностно-статистический подход к моделированию коррозионного разрушения. Необходимость такого подхода отмечалась в работе А.Р. Ржаницына [96]. Следует также отметить статьи В.Я. Флакса, И.А. Прыткина [90, 91, 106], в которых с использованием данного подхода определялись напряженно-деформированное состояние и долговечность конструкций, подвергающихся воздействию коррозионных сред. В работах С.А. Тимашева [100, 101] оценивалась надежность пластин и оболочек, подвергающихся коррозионному износу. В статьях В.Д. Райзера с соавторами [50, 93 – 95] уделяется большое внимание разработке теории надежности конструкций, подвергающихся коррозионному износу. В статье Р.Г. Маннапова [52] распределение глубин коррозионных повреждений подчиняется закону Вейбулла – Гнеденко, в его же статьях [51, 53] выявлен вид функции распределения глубин по поверхности металлов и изменение во времени характерных параметров.
Р.А. Арутюнян [2] рассмотрел задачу разрушения тонкостенной оболочечной конструкции вследствие питтинговой коррозии, при этом принималось, что начальное распределение питтингов по поверхности конструктивного элемента является случайным, случайно также время появления первого отверстия. Глубина питтингов контролируется процессами электрохимической коррозии. Вычисляется функция надежности и сформулирован критерий разрушения (образования первого коррозионного отверстия), учитывающий механохимические процессы разрушения.
В области строительства и архитектуры решению задач оптимального проектирования с дополнительным учетом вероятностного характера отказа конструкций, подверженных влиянию агрессивной среды, посвящены работы И.Г. Овчинникова [59]. Р.М. Магометова [49], A.J.M. Siemes и др. [125], в которых рассматриваются оптимизация и надежность железобетонных конструкций и трубопроводов.
В завершении теоретической части обзора отметим, что различные аспекты влияния агрессивной среды на характеристики деформирования и разрушения современных металлов и сплавов рассматриваются в большом количестве монографий ([1, 4, 5, 6, 7, 8, 11, 22, 23, 34, 36, 37, 54, 55, 72, 74, 78, 81, 84, 85, 86, 89, 96, 97, 99, 101, 104, 112, 114, 115, 117, 119] и др.) и журнальных статей, в том числе обзорного характера, например, [33, 38].
Экспериментальные работы
Сначала отметим ряд экспериментальных исследований, которые проведены в ЦНИИ «Прометей» (г. Санкт-Петербург) и опубликованы в журнале «Вопросы материаловедения» [17, 24, 25]. Эти работы связаны с экспериментальным исследованием ползучести и длительной прочности материалов и элементов конструкций оборудования атомных электростанций, находящихся в контакте с жидкометаллической агрессивной средой. Далее в настоящей статье приводится обзор этих работ с акцентированием внимания на полученных исследователями экспериментальных зависимостях характерных параметров коррозионного процесса и длительной прочности от времени.
А.С. Кудрявцев, В.Г. Марков и В.С. Лаврухин [25] рассмотрели вопросы длительной прочности конструкционных материалов, работающих в реакторной установке с жидкометаллическим свинцовым теплоносителем. Рабочая температура жидкометаллического теплоносителя на основе свинца превышает 500 °С, т.е. находится в диапазоне температур, при которых в сталях могут интенсивно протекать процессы ползучести. Авторы статьи отмечают, что недостатком теплоносителей на основе свинца является их агрессивность по отношению к конструкционным материалам [17], мерой по борьбе с этой агрессивностью является поддержание определенной концентрации кислорода в жидком теплоносителе. В результате на поверхности стали образуется оксидная пленка, предотвращающая контакт материала с жидкометаллическим теплоносителем. В работе приведены экспериментальные данные, полученные при длительных испытаниях образцов двух марок сталей 10X15Н9С3Б и 10Х9НСМФБ, а именно, приводятся данные по длительной прочности образцов этих марок стали на воздухе и в потоке жидкого свинца. В результате показано, что длительная прочность образцов, испытанных в потоке жидкого свинца, ниже длительной прочности образцов, испытанных на воздухе. Причины снижения длительной прочности в жидком свинце были выявлены в ходе металлографического анализа, который показал, что при высоком уровне напряжений на образцах имеются следы фронтальной жидкометаллической коррозии. При уменьшении уровня напряжений на образцах наблюдается плотная оксидная пленка, сплошность которой нарушается тем сильнее, чем ближе она к месту разрушения образца. Эта пленка защищает образец от агрессивного воздействия окружающей среды, причем ее толщина зависит от уровня напряжений и длительности контакта с жидким металлом. В статье приведена таблица скорости окисления исследуемого металла под нагрузкой и без нагрузки, кроме того, приведен график зависимости толщины оксидной пленки от длительности испытаний образцов указанных двух марок сталей при температуре 550 °С. Авторы отмечают, что первоначально предполагалось, что снижение длительной прочности в этом случае обусловлено уменьшением сечения образца за счет процессов окисления. Однако при более длительных испытаниях прямая зависимость степени снижения длительной прочности от уменьшения площади сечения образца не отмечалась. Более детальное исследование множества трещин на поверхности оксидных пленок с помощью растрового микроскопа с приставкой для микрорентгеноспектрального анализа показало, что эти трещины проходят не только сквозь оксидную пленку, но и сквозь слой внутреннего окисления металла, причем их вершины являются местом контакта внутреннего слоя материала и свинцового жидкометаллического теплоносителя. В заключении статьи отмечено, что снижение длительной прочности образцов, испытанных в жидком свинце, при высоких уровнях напряжений обусловлено процессами фронтальной жидкометаллической коррозии, при более низких – совокупным влиянием процессов окисления, образования трещин в оксидной пленке и проникновения в них жидкого свинца. При использовании результатов испытаний образцов без следов фронтальной жидкометаллической коррозии прогнозировать длительную прочность материалов, работающих в жидкометаллическом теплоносителе на основе свинца, можно с помощью линейной экстраполяции аналогично прогнозированию длительной прочности материалов, работающих на воздухе.
В работе [24] исследовано влияние жидкометаллического свинцового теплоносителя на ползучесть хромистой мартенситной стали марки 10Х9НСМФБ. При проведении испытаний на длительную прочность отмечена повышенная скорость ползучести стали в контакте с жидким свинцом при температуре 550оС по сравнению со скоростью ползучести на воздухе. В статье приводятся результаты экспериментов и их обсуждение. Авторы отмечают, что в целом скорость ползучести образцов, испытанных в потоке жидкого свинца, превышает скорость ползучести образцов, испытанных на воздухе. Однако, если при высоком уровне напряжений этот эффект наблюдается непосредственно в начале испытаний (рисунок, а), то снижение уровня напряжений приводит к совпадению кривых ползучести на первой и частично на второй стадиях ползучести (рисунок, б). Начавшееся после испытаний в течение 10 тыс. час ускорение ползучести свидетельствует не о начале третьей стадии ползучести, а об изменении ее скорости на второй стадии.
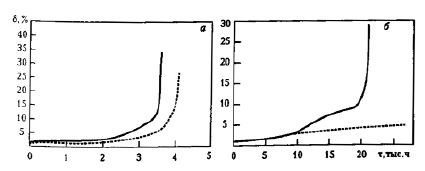
Кривые ползучести стали марки 10Х9НСМФБ при температуре 550 °С в потоке жидкого свинца (сплошная линия) и на воздухе (штриховая линия): а) напряжение 98 МПа (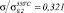 ); б) напряжение 68,6 МПа (
); б) напряжение 68,6 МПа (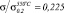 )
)
Авторы объясняют, что различное поведение кривых ползучести образцов, испытанных в контакте с жидким свинцом и на воздухе при уровне напряжений 98 Мпа и 68,6 МПа, а также данные металлографического анализа образцов, разрушенных в потоке жидкого свинца, свидетельствуют о наличии двух принципиально различных механизмов разрушения образцов в контакте со свинцовым теплоносителем. Это явление, обнаруженное в работе [25], связано с влиянием уровня напряжений на устойчивость оксидных пленок. В заключении авторы отмечают, что для повышения надежности реакторной установки с жидкометаллическим теплоносителем на основе свинца при расчете максимально допустимых напряжений в конструкциях, работающих в контакте с жидким свинцом, рекомендуется учитывать пределы ползучести конструкционных материалов, вводя ограничения по допустимой деформации на выбранной временной базе.
Помимо исследований, описывающих влияние жидкометаллической среды на длительные свойства сталей, сотрудниками ЦНИИ «Прометей» проведены исследования о влиянии этой среды на циклическую долговечность материалов.
В работе Л.И. Огородов и А.С. Белов [82] привели результаты экспериментально-теоретического исследования длительной прочности сплава ЭИ893ВД при кусочно-постоянных напряжениях в двухкомпонентной агрессивной среде, а именно, как в воздушной среде, так и в солевой газовой среде. Агрессивность среды характеризуется солевой нагрузкой ks, представляющей собой весовое количество солей, оседающих на единицу площади на поверхности элемента конструкции в единицу времени. Учет влияния агрессивной среды на длительную прочность осуществляется в [82] введением коэффициента ks в определяющие уравнения. Этот метод хорошо описывает экспериментальные данные, полученные в случае агрессивной среды одного и того же состава, однако он не подходит для анализа результатов испытаний одного и того же сплава в агрессивных средах различного состава.
В статье азербайджанских авторов Р.А. Кязимовой и Э.Т. Багирова (Институт математики и механики Национальной Академии Наук Азербайджана) [28] предложена эмпирическая формула, которая позволяет аналитически описывать экспериментальные кривые коррозионного разрушения под напряжением при учете влияния температуры. Сформулирована система опытов с целью определения универсальных констант системы «металл – коррозионная среда». Представлены результаты обработки опубликованных в литературе некоторых экспериментальных данных по коррозионному разрушению. На рисунках в статье приведены экспериментальные и расчетные кривые коррозионной прочности α-латуни в растворе аммиака (плотность 0.94) и армировочной бетонной проволоки в 10 процентном растворе роданистого аммония и мартенситной стали (0,14 % С) в 80 % растворе нитрата кальция.
Заключение
Проведенный обзор исследований по моделированию процессов взаимодействия агрессивной среды с материалами и элементами конструкций показал широкое разнообразие и развитие подходов и методов теоретико-экспериментальных исследований в несомненно актуальной и важной области взаимодействия материала элементов конструкций и внешних факторов, влияющих на их служебные свойства. Как известно, указанное взаимодействие оказывает влияние на механические, физические, химические, электротехнические и другие характеристики материала.
Сложность рассматриваемых явлений, широта их многоуровневой реализации обусловливает самый главный вывод: междисциплинарность научных подходов к изучению этих явлений. Такие междисциплинарные научные подходы влекут необходимость построения адекватных физико-химических и механико-математических (феноменологических) моделей, позволяющих описать явление, выделить основные параметры, влияющие на процессы взаимодействия материала и агрессивных сред, и построить адекватные модели, которые позволят спрогнозировать поведение материалов, отдельных элементов и конструкции в целом в течение всего срока эксплуатации. Предлагаемые исследователями механико-математические модели должны базироваться на основных гипотезах механики деформируемого твердого тела и дополнительно учитывать физико-химические процессы, происходящие в материале.
В результате проведенного обзора авторы настоящей статьи отмечают следующие основные направления и подходы, которые представляют особый интерес для дальнейшего научного развития. Это упомянутый ранее научный подход британского ученого J. Crank [119], учитывающий модификацию классического параболического уравнения диффузии (2). Интересен подход И.Г. Овчинникова [63], учитывающий конкуренцию распространения (различие скоростей диффузии и химической реакции) областей диффузионного проникновения и химического превращения агрессивной среды в материале. Кроме того, представляет научный интерес для дальнейшего развития подход И.Г. Овчинникова [76], в котором используется параметр химического взаимодействия q, определяемый либо уравнением (3), либо уравнением (5). Также важна работа И.Г. Овчинникова [77], учитывающая градиент напряжений в модифицированном уравнении диффузии (7) водородосодержащей среды, а компоненты тензора напряжений и тензора деформаций связаны соотношениями, коэффициенты которых зависят от концентрации агрессивной среды c в материале и характеристики вида напряженного состояния 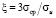 , σcp – среднее напряжение, σu – интенсивность напряжений.
, σcp – среднее напряжение, σu – интенсивность напряжений.
В заключении также необходимо отметить, что в настоящее время существует достаточно большое количество работ и исследований по рассматриваемой теме. В настоящей статье отражена лишь часть этого множества работ, определяющая основные научные направления.
Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований, номер гранта № 17-08-00210а.
 science-review.ru
science-review.ru