Scientific journal

Название журнала на английском

ISSN 2500-0802

ПИ №ФС77-61154

Во всем мире наблюдается тенденция движения от индустриального к информационному обществу. Считают, что в скором времени будет построена новая экономика, основанная на знаниях [23]. Новые подходы требуют рассмотрения соответствующей инфраструктуры нового экономического общества, иначе говоря, его киберинфраструктуры.

Все сказанное в полной мере относится и к медицинской сфере. При решении задач медицинской диагностики и прогнозирования всегда следует учитывать необходимость жестких ограничений времени на обследование и постановку диагноза. Особенно это касается неотложных случаев, а также при использовании медицинских информационных систем во время массовых профилактических осмотров населения. Перспективным следует рассматривать возможности использования ГИС и ГРИД технологий, облачных сервисов для решения широкого круга медицинских задач. И здесь не обойтись без разработки, так называемых, высокопроизводительных вычислений с использованием суперкомпьютеров. Без суперкомпьютеров практически невозможны серьезные прорывы в таких областях науки, как биология и медицина. Нужна помощь суперкомпьютеров и при моделировании человеческого сердца, мозга и других живых систем в области биоинформатики.

В настоящее время рассматривается необходимость решения прикладных задач совместимости суперкомпьютера и медицинской аппаратуры. Это позволит в режиме реального времени анализировать состояние больных, определять точный диагноз и оптимальный путь лечения.

Причиной снижения качества жизни и увеличения смертности населения развитых стран мира являются основные и известные сердечнососудистые заболевания: ИБС, ревматические митральные пороки, диффузный токсический зоб, артериальная гипертензия (гипертрофии левого желудочка), пролапсе митрального клапана, миокардит, перикардит, первичные и вторичные кардиомиопатии [36].

Появление в течение основного заболевания фибрилляции предсердий отрицательно сказывается на параметрах качества жизни больных, уменьшается переносимость физической нагрузки, возникает сердечная недостаточность, при МА у больных в 5-7 раз чаще наблюдаются инсульты мозга. По данным института мозга во Франции, 50% инсультов мозга возникают вследствие кардиоэмболии, при этом в 40% случаев имеется постоянная или пароксизмальная мерцательная аритмия, 30% таких больных умерли в течение последующих 6 месяцев.

В клинической практике помимо лекарственной терапии фибрилляции предсердий весьма эффективно используют электроимпульсную терапию (ЭИТ). В последние годы стали использовать и хирургические методы лечения синдрома фибрилляции предсердий, связанные с прерыванием «порочного круга» проведения возбуждения, а именно: «Лабиринтный», «Коридорный» и радиочастотной катетерной аблации (деструкции).

Для каждого из способов восстановления синусового ритма необходим прогноз возможности восстановления и сохранения синусового ритма на протяжении не менее чем шести последующих месяцев. Для реализации этих двух задач необходим прогноз полезности восстановления синусового ритма над риском эмболических осложнений и возможных рецидивов мерцания.

Решение проблемы полезности восстановления синусового ритма, основанное на общеклинических критериях исследования относится к трудоемким и субъективным методам, обеспечивающим маловоспроизводимые результаты в силу отсутствия разработанных стандартов в критериях оценок.

Следовательно, актуальными являются поиски математических критериев и способов прогнозирования восстановления синусового ритма.

Рассмотрим основные направления разработки вычислительных методов диагностики применительно к кардиологии.

Со второй половины прошлого века наблюдается проникновение математических методов в теорию и практику медицины. В настоящее время эта тенденция укрепляется все больше и больше. Подобное слияние научных направлений позволяет получить качественно новые результаты, недостижимые при использовании традиционных способов врачебной диагностики [10, 75, 77, 78].

Врачебные алгоритмы диагностики относят к эвристическим процедурам. Многие методики обучения диагностике заболеваний носят эмпирический характер. При этом большое значение имеет «опыт» и «интуитивный» подход к диагностике, что может привести к ошибке и, как следствие, к выбору некорректных методов лечения [25, 26].

Еще с конца прошлого века было подмечено, что автоматизация диагностических процессов при правильной постановке медицинских задач и формировании репрезентативных обучающих выборок позволяет в ряде случаев получить существенное повышение точности диагностики [39]. В настоящее время технические и программные средства дают качественно новые возможности обработки медицинских данных [34, 46, 64].

Выделим некоторые проблемы, специфичные для задач медицинской диагностики, которые затрудняют применение объективных математических методов.

1. Врачи вынуждены оперировать неполными и не всегда достаточно определенными классификациями заболеваний.

2. Некоторые классы заболеваний пересекаются. Часто у больных наблюдается сочетание различных заболеваний, что приводит к нетипичной клинической картине.

3. Диагностическая информация может быть не всегда всеобъемлющей, в связи с тем, что ряд сложных диагностических приемов не может быть применен у здоровых людей и больных с ранними стадиями заболевания из-за опасности их использования для здоровья и жизни обследуемых лиц.

3. Темпы развития патологического процесса и особенности клинических проявлений различны у каждого пациента. При этом о многих патологических состояниях приходится судить еще и по косвенным признакам.

4. Исторически сложилось так, что накопление статистических сведений о ряде заболеваний осуществлялось эмпирически без достаточного учета однородности выборок, характеристик используемой аппаратуры и методик исследования. Практически отсутствуют сведения о вероятности заболеваний при наличии тех или иных симптомов или синдромов. Выбор врачебных признаков на практике, как правило, осуществляется без количественной оценки их информативности.

5. Форма представления врачебных признаков часто не соответствует языку вычислительных систем. Отсутствие точных количественных критериев требует формализации врачебных признаков для целей автоматической диагностики.

Учитывая выше изложенное, отметим, что во многих задачах медицинской диагностики редко удается задать перечень классов, которые удовлетворяли бы требованиям полноты (каждый объект основной совокупности обязан принадлежать к одному из заранее заданных классов) и непересекаемости (каждый объект основной совокупности принадлежит только одному классу).

Частным случаем автоматической диагностики является применение математических методов для анализа электрокардиограмм (ЭКГ).

Ряд исследователей [7, 47, 59, 74] считают, что разработка алгоритмов и программ для моделирования нормальной деятельности и различных нарушений ритма и проводимости является весьма перспективной задачей, поскольку математическое моделирование позволяет раскрыть новые черты патогенеза некоторых нарушений ритма и проводимости.

Алгоритмы автоматической классификации ритма сердца различаются по характеру и числу используемых электрокардиографических признаков, числу диагностируемых классов и виду, решающих правил. Электрокардиографическими признаками считают отсчеты и параметры ЭКГ, а также любые величины, рассчитываемые по ним, используемые в процессе распознавания.

Некоторые исследователи для этих целей предлагают вариант порогового алгоритма обнаружения QRS-комплекса, на вход которого подаётся взятый по модулю сигнал с выхода предложенного выделителя желудочкового комплекса [22]. Показано, что при отсутствии существенных помех и низкоамплитудных QRS-комплексов, такой алгоритм способен эффективно обнаруживать желудочковые комплексы на фоне других компонентов ЭКГ. В то же время автор отмечает, что «для практического использования в системах кардиологического контроля необходимо применение более сложных алгоритмов, обладающих способностью к адаптации и к учёту контекста электрокардиосигнала»

Другие авторы [33] указывают на то, что «распознавание фрагментов мерцательной аритмии, представленных последовательностями кардиоинтервалов конечной длины, целесообразно проводить с использованием скорректированных оценок условной энтропии и приближенной оценки энтропии Колмогорова, что делает возможным анализ динамики хаотических свойств анализируемых процессов в режиме реального времени»

В связи, с чем многими исследователями был изучен сложнопериодический характер изменений параметров биосистем с использованием методов детерминированной хаотической динамики и анализа стохастических аттракторов в кардиологии [19, 80, 84].

Известно, что стохастичность характерна для систем, в которых возможны колебания, вызываемые наличием обратной связи. Этот подход позволил вплотную подойти к разгадке слабых взаимодействий. Был показан механизм того, как, например, стохастические системы с фликкер-шумом могут ответить максимальной реакцией на минимальное возмущение.

В последнее десятилетие рассмотрено много различных подходов к изучению ритма сердца и ритма дыхания, базирующихся на методах нелинейной динамики. Так, известен метод нелинейной символической динамики [15, 16, 85], который также используется с кодированием «слов» разной нефиксированной длины, в том числе для диаграмм рассеивания минимумов и максимумов RR – интервалов ЭКГ. По мнению цитированных авторов, эти методы позволяют выявить наиболее значительные отличия здоровых и больных людей даже в периоды отсутствия внешних неблагоприятных воздействий.

Как оказалось выявление утраты меры влияния синусового узла при мерцательной аритмии позволяет прогнозировать результаты применения дефибрилляции предсердий, или использования антиаритмических препаратов [43]. Решение проблемы полезности восстановления синусового ритма, основанное на общеклинических критериях исследования относится к трудоемким и субъективным методам, обеспечивающим маловоспроизводимые результаты в силу отсутствия разработанных стандартов в критериях оценок [30, 46].

Для целей классификации нарушений синусового ритма разными авторами описаны методы условно-вероятностного анализа, корреляционной ритмографии, скаттерографии [9, 42, 58, 79].

Известны способы автоматизации данных методов [8, 11, 12, 14, 35]. В них предварительно обработанную информацию в виде авторегрессионных облаков предъявляют врачу-эксперту, который и дает заключение о конечном прогнозе, либо прогноз реализуется в автоматическом режиме [24, 40, 44].

Впервые в 1995 году Ф.А. Пятаковичем на основании нечетких множеств был описан алгоритм дифференциации авторегрессионных облаков у больных с синдромом фибрилляции предсердий [54].

В [66] были получены адекватные модели и алгоритмы автоматического распознавания авторегрессионных облаков с использованием элементов теории нечетких множеств с использованием программного генератора для формирования скатерограмм.

В [62,65] описан геометрический алгоритм распознавания класса авторегрессионного облака, базирующийся на поиске сгущения точек в заданной экспертом зоне.

Алгоритмы распознавания авторегрессионных облаков, описанные в [48, 63, 72], используют разделение гиперплоскостью мономодальных и немономодальных классов на основе выделенных информационных признаков оценки микроструктуры и макроструктуры ритма.

Однако эти исследования носили больше экспериментальную и методологическую направленность, нежели клиническую [50].

К методам автоматической диагностики, обладающим способностью к адаптации и к учёту контекста электрокардиосигнала, прежде всего, относятся искусственные нейронные сети [57, 73, 82]. Ряд авторов успешно применяют «нейрокомпьютинг» для решения задач диагностики у больных с синдромом фибрилляции предсердий [6, 21, 37, 70].

В экспертных системах процесс принятия решений базируется на методах дедукции, индукции, аналогии и генерации гипотез. Одним из научных фундаментов экспертных систем распознавания являются искусственные нейронные сети [38].

Единицей обработки информации в сети выступает искусственный нейрон, в состав которого обычно входят синаптические веса, сумматор и функция активации (рис. 1).

На вход нейрона подается входной вектор 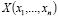. Каждая координата входного вектора ослабляется или усиливается умножением на синаптический весовой коэффициент , .

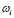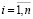Сумматор складывает входные сигналы, взвешенные относительно соответствующих синапсов нейрона. Выходом блока суммирования является линейная комбинация входных сигналов:

.

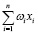Функция активации (сжатия) ограничивает амплитуду выходного сигнала нейрона. Нормализованный диапазон амплитуд выхода блока нелинейного преобразования принадлежит отрезку [0,1] или [-1,1].

Часто используются такие функции активации, как пороговая (рис. 2), кусочно-линейная (рис. 3), сигмоидальная (рис. 4) и гиперболический тангенс (рис. 5).

Модель нейрона с пороговой функцией активации называют моделью Мак-Каллока – Питтца, отдавая дань пионерской работе. Выбранный вид функции активации описывает ключевое свойство модели Мак-Каллока – Питтца: «всё или ничего».

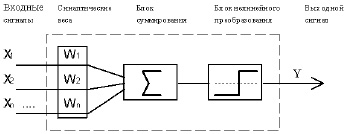
Рис. 1. Схема искусственного нейрона

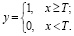
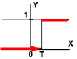
Рис. 2. Функция единичного скачка или пороговая функция (функция Хевисайда)

Аргументом х пороговой функции является выходной сигнал блока суммирования, называемый также индуцированным локальным полем нейрона.

Величина Т определяет пороговый уровень, начиная с которого нейрон возбуждается, что соответствует появлению единичного значения на выходе нейрона.

При использовании кусочно-линейной функции активации обеспечивается плавный линейный переход выходного значения из нуля в единицу при нарастании возбуждения нейрона.

Наиболее распространенными функциями активации являются сигмоидальная функция и гиперболический тангенс, поскольку они являются дифференцируемыми и их производные выражаются через значения самих функций.

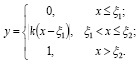
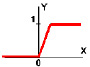
Рис. 3. Кусочно-линейная функция активации

Сигмоидальная функция активации имеет вид:

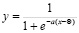. (1)

Сигмоидальная функция обеспечивает нелинейный, «S» – образный переход выходного значения из нуля в единицу при нарастании возбуждения нейрона. Параметр а управляет уровнем наклона графика активационной функции. Порог Θ определяет точку перегиба графика.

Разновидностью сигмоидальной функции является логистическая функция.

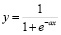
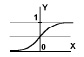
Рис. 4. Логистическая функция активации

Сигмоидальная функция поддерживает баланс между линейным и нелинейным поведением нейрона.

Если требуемый диапазон выходного сигнала принадлежит отрезку [-1;1], то в качестве функции активации нейрона используют гиперболический тангенс.

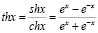
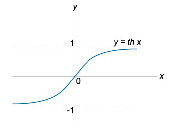
Рис. 5. Гиперболический тангенс

Схематически искусственные нейронные сети представляют в виде графов (рис. 6).

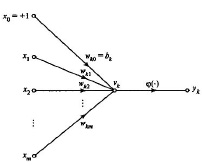
Рис. 6. Граф передачи сигнала внутри нейрона

Искусственную нейронную сеть можно представить в виде направленного графа, состоящего из узлов, соединенных синаптическими и активационными связями [61].

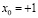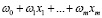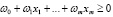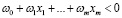Для улучшения процесса сходимости на вход нейрона подается тождественный сигнал . В этом случае выходной сигнал сумматора имеет вид . Пусть для пороговой функции активации Т=0. Тогда условия и позволят разделить точки двух классов пространства .

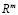При использовании комбинации линейных нейронов в гиперпространстве очерчиваются многогранники, разделяющие входные значения разных классов [68].

В схематическом изображении взаимодействия различных элементов нейронной сети, подробности прохождения сигнала внутри отдельного нейрона опускают. Такие схемы называют архитектурными (рис. 7).

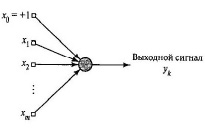
Рис. 7. Архитектурный граф нейрона

Основными архитектурами искусственных нейронных сетей являются модели однослойных и многослойных сетей прямого распространения сигнала, а также рекуррентные сети с обратным направлением прохождения сигнала [61].

В однослойной сети информация от входного слоя 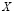передается на выходной слой нейронов 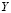. Сеть называется однослойной, потому что в ней один слой вычислительных узлов 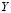, служащих элементами обработки информации (рис. 8).

Синаптические коэффициенты в однослойной сети являются элементами матрицы 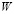размера .

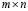В двухслойной сети есть скрытый слой нейронов. Сеть на рис. 9 называется 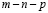сетью, поскольку в ней 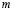входных элементов, 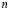скрытых нейронов и 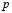выходных нейронов. В такой сети две матрицы синаптических коэффициентов: матрица связей между входными элементами и скрытыми нейронами 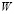размера 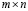и матрица связей между скрытыми и выходными нейронами 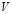размера .

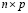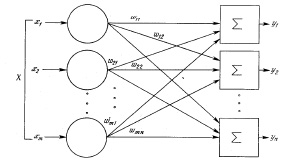
Рис. 8. Однослойная сеть прямого распространения

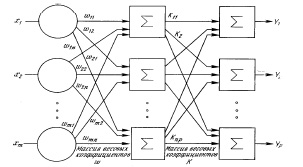
Рис. 9. Двухслойная сеть прямого распространения

В многослойных сетях имеется несколько слоев скрытых нейронов. Такие сети способны выявлять более сложные статистические закономерности между входными и выходными величинами.

В рекуррентных сетях имеются обратные связи (рис.10). В таких сетях сигнал многократно передается с выходов нейрона обратно на их входы, вызывая циклические изменения состояния нейронов.

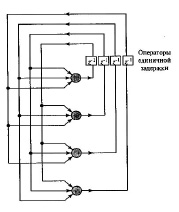
Рис. 10. Рекуррентная сеть

На рис. 10 показана архитектура сети, состоящей из одного слоя нейронов, каждый из которых направляет свой выходной сигнал на входы остальных нейронов слоя. В приведенной архитектуре отсутствуют обратная связь нейрона с самим собой.

Прежде чем использовать искусственную нейронную сеть в режиме функционирования (решения задачи), её требуется обучить. Целью процесса обучения является вычисление значений синаптических (весовых) коэффициентов [1, 34].

Концепция «обучения с учителем» предполагает наличие обучающей выборки.

Обучающая выборка состоит из пар векторов. Каждая пара включает входной вектор и целевой вектор, представляющий собой желаемый отклик сети при подаче на ее входы координат данного входного вектора, описывающего состояние среды.

В процессе обучения на выходах сети вычисляются текущие сигналы, называемые фактическим откликом сети.

Фактический отклик сравнивается с желаемым откликом сети (рис. 11). По результатам сравнения вычисляется сигнал ошибки, который учитывается при коррекции весовых коэффициентов [61].

В роли «учителя» для искусственной нейронной сети выступает эксперт, определяющий для обучающей выборки входных векторов, желаемые отклики сети.

Целью обучения является получение набора весовых коэффициентов, при котором достигается минимум ошибки между фактическим и желаемым откликами сети на множестве входных векторов из обучающей выборки.

Фактически при обучении сети подбираются значения её внутренних параметров, обеспечивающих имитацию принятия сетью решений, наиболее близких к мнению эксперта.

Канадский биолог Д. Хебб сформулировал первое правило обучения искусственной нейронной сети: если два нейрона возбуждаются одновременно, то сила синаптической связи между ними увеличивается, если возбуждение происходит асинхронно, то уменьшается.

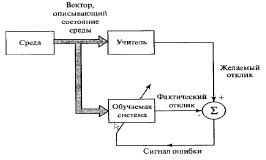
Рис. 11. Схема концепции «обучение с учителем»

В [70] описан метод решения задачи прогнозирования исходов мерцательной аритмии, основанный на моделировании однослойной нейронной сети прямого распространения, обученной по правилу Хебба

Метод корреляционной ритмографии позволяет разделить больных с синдромом фибрилляции предсердий на несколько функциональных классов в зависимости от типа авторегрессионного облака:

1. Мономодальный симметричный.

2. Мономодальный асимметричный.

3. Мономодальный инвертированный.

4. Полимодальный.

5. Амодальный.

Авторегрессионное облако (АРО) – это совокупность точек (RRi, RRi+1), где 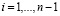; 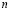– количество 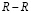интервалов на электрокардиограмме. В зарубежной литературе эту совокупность точек называют скаттерграммой или авторегрессионным облаком, а в отечественной литературе используют название – корреляционная ритмография, или сокращенно КРГ [76].

С 1970 года И.И. Красовский использовал КРГ для разработки алгоритмов автоматического анализа ритма сердечной деятельности.

При наличии правильного ритма сокращения желудочков скопление точек образуется на биссектрисе координатного угла. При стойкой ритмичности – стабильном ритме – основная совокупность превращается в точку на биссектрисе. Умеренная синусовая аритмия приводит к образованию авторегрессионного облака в виде эллипса (рис. 12) или круга.

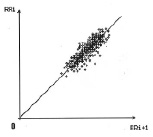
Рис. 12. АРО пациента с умеренной синусовой аритмией

При благоприятном прогнозе на восстановление синусового ритма точки АРО группируются на сравнительно ограниченной округлой площади, выраженное сгущение наблюдается вблизи биссектрисы координатного угла (рис. 13).

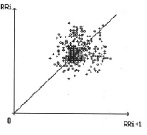
Рис. 13. АРО мономодального симметричного класса

Сгущение может быть в центре (рис. 13), в левом нижнем (рис. 14) и правом верхнем углу АРО (рис. 15).

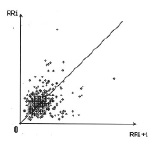
Рис. 14. АРО мономодального асимметричного класса

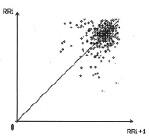
Рис. 15. Авторегрессионное облако мономодального инвертированного класса

При сомнительном прогнозе на восстановление синусового ритма на АРО образуется несколько симметрично расположенных относительно биссектрисы совокупностей точек (рис. 16), либо имеет место широкое рассеивание точек на плоскости (рис. 17).

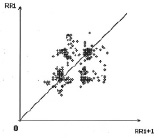
Рис. 16. АРО полимодального класса

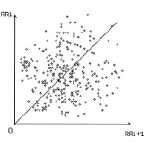
Рис. 17. АРО амодального класса

Таким образом, выраженная аритмичность сокращения желудочков, сопровождающая мерцание предсердий, проявляется на корреляционной ритмограмме широким рассеиванием точек на плоскости. Наблюдения показали, что полная беспорядочность чередования межпульсовых интервалов при мерцании предсердий является кажущейся.

Наличие выраженного сгущения точек на биссектрисе координатного угла является прогностически благоприятным и свидетельствует о вполне удовлетворительном функциональном состоянии сердца. Имеется предположение о возможности влияния синусового узла на ритм желудочков, регулируемый в обход мерцающих предсердий через межузловые тракты.

Таким образом, мономодальные типы (рис. 13-15) свидетельствует об удовлетворительных функциональных возможностях синусового узла. Прямым подтверждением справедливости этого утверждения является эффективность восстановления и удержания синусового ритма у больных с такими типами АРО.

При полимодальном типе облака точки группируются вблизи биссектрисы параллельно осям координат в виде отдельных скоплений (рис. 16). В зависимости от расстояния между центрами скоплений выделяют два подтипа: 1 – трепетание предсердий с меняющимся атриовентрикулярным проведением; 2 – крупноволновая форма фибрилляции предсердий.

У облака амодального типа (рис. 17) сгущение точек вблизи биссектрисы отсутствует. В данном случае функциональное состояние синусового узла неудовлетворительно и перспективы на восстановление правильного синусового ритма сомнительны.

Считается, что тип АРО отражает степень утраты регуляторных воздействий на ритм сердца при мерцательной аритмии: достаточное сохранение при первом типе, меньшее – при втором, наименьшее – при третьем типе. У больных с третьим типом АРО, которому сопутствует большой разброс точек, не удается сохранить восстановленный синусовый ритм на срок до 6 месяцев. Переходной формой между трепетанием и мерцанием предсердий является четвертый тип облака.

Границы между дифференцируемыми классами размыты, особенно это касается асимметричных и низкомодальных типов АРО.

В работе [70] описана однослойная искусственная нейронная сеть прямого распространения сигнала, состоящая из пяти нейронов, каждый из которых в процессе обучения настраивается на представление одного из классов АРО.

Входной слой сети является моделью сенсорных клеток, принимающих двоичные сигналы от внешнего мира. На вход нейронной сети поступают бинарные прямоугольные изображения АРО.

Во входной слой включается m нейронов 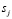, где j=1,...,m, где m – количество точек на изображении.

Если на изображении точка черная, то нейрон считается активным. В этом случае значение элемента одномерного массива, реализующего входной слой, равно 1. Если на изображении точка белая, то нейрон неактивен и значение соответствующего элемента массива равно 0.

Входной слой является моделью сенсорных клеток, принимающих двоичные сигналы от внешнего мира. В дальнейшем сигналы поступают в слой ассоциативных клеток (выходных нейронов) 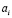, где 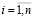, которые имеют изменяемые веса связей с сенсорными клетками (рис. 18).

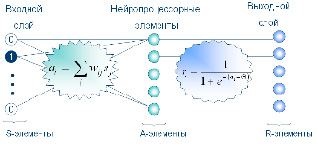
Рис. 18. Архитектурная схема сети для автоматического распознавания класса АРО

Активность i-й ассоциативной клетки определяется формулой:

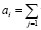wij sj, (2)

где wij – коэффициент связи между i-й ассоциативной клеткой и j-й сенсорной клеткой.

Информация от ассоциативных клеток подлежит нелинейной обработке, в результате которой формируется реакция сети на входной образ. Для вычисления активности нейрона выходного слоя 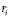, где i=1,..,n, используется сигмоидальная функция активации.

Узнавание класса проводится по самому возбужденному нейрону выходного слоя.

Перед обучением сети эксперт проводит классификацию АРО из обучающей выборки, определяя класс, к которому следует отнести данный элемент.

В процессе обучения случайным образом определяется номер облака из обучающей выборки. По номеру входного примера восстанавливается номер класса i, к которому было отнесено данное облако экспертом. В целевого вектора 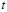только i-я координата равна единице, а все остальные координаты равны нулю.

По выбранному элементу обучающей выборки вычисляется активность нейронов входного слоя, ассоциативных клеток и нейронов выходного слоя.

Для каждого класса вычисляется вектор ошибки:

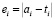. (3)

Суммарная ошибка сети вычисляется по формуле:

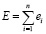. (4)

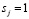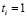Весовые коэффициенты модифицируются с учетом ошибок по классам согласно правилу Хебба. При этом усиливается связь между черными точками и ассоциативной клеткой, соответствующей номеру “своего” класса: если и , то

wij = wij + c ⋅ ei,

где 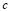– константа, влияющая на скорость и качество обучения.

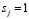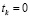Ослабляется связь между черными точками и ассоциативными клетками, отвечающими за “чужой” класс: если и , то

wik = wik – c ⋅ ek,

где .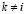

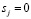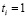Ослабляется связь между белыми точками и ассоциативной клеткой, отвечающей за “свой” класс: если и , то

wij = wij – c ⋅ ei.

Обучающие сеансы повторяют до тех пор, пока суммарная ошибка сети не станет меньше некоторой константы или не закончится обучающая сессия (рис. 19).

Лучший результат обучения (матрица весовых коэффициентов, с которыми сеть сделала минимальную ошибку в распознавании элементов обучающей выборки) сохраняется в файл. При загрузке весовых коэффициентов из файла можно проводить последовательное обучение сети в режиме off-line.

В исследовании [13] было установлено, что точка локального минимума не единственна. АРО из обучающей выборки распознаются в 100% случаев правильно. АРО мономодальных классов из контрольной выборки также были распознаны в 100% случаев правильно. Ошибка распознавания АРО немономодальных классов из контрольной выборки составила 8%.

Рис. 19. Алгоритм обучения сети автоматическому распознаванию класса АРО

В научных работах [2-5, 20] для исследования вариабельности сердечного ритма были использованы многослойные нейронные сети, реализованные в Matlab.

В последние годы широкое развитие получили технологии реабилитационного лечения психосоматических заболеваний, основанные на использовании биологической обратной связи. Среди них успешно применяется и биоуправляемый игровой тренинг для коррекции стрессиндуцированных состояний у лиц опасных профессий, в спортивной практике, для лечения психосоматических заболеваний, а также для реабилитационного лечения детей, страдающих синдромом гиперактивности и дефицита внимания [27, 28, 83].

В процессе проводимого биоуправляемого игрового тренинга постоянно сохраняется необходимость оценки объективного состояния ведущих физиологических систем организма пациента в режиме on-line. Для этих целей авторами [28, 52] использован хронодиагностический алгоритм непрерывного отслеживания отношений периодов пульса и дыхания.

В работе [60] предложена система правил нечёткого вывода, отличающихся возможностью выделения различных классов функциональных состояний человека с определением количественных характеристик их уровня, составивших основу построения базы знаний для соответствующей системы поддержки принятия решений. Кроме объективных данных, снимаемых с обследуемого специализированными аппаратными средствами, в процессе диагностики функционального состояния используются также данные опроса, осмотра и инструментальных исследований.

Известно, что регулирование параметров, избранных для мониторинга при биоуправлении, в обычных условиях реализуется за счет сочетанной деятельности нескольких координирующих и пусковых иерархических систем [55, 56].

В исследованиях [29, 53] рассмотрены модельные представления об иерархии управления регуляцией частотой сердечных сокращений, включающей шесть режимов:

1) детерминированный;

2) квазидетерминированный;

3) гармонический;

4) квазигармонический;

5) квазистохастический;

6) стохастический

Указанные математические модели позволяют, во-первых, выделить и прогнозировать динамику того или иного параметра, относящегося к механизмам регуляции частоты сердечных сокращений в условиях перманентного воздействия извне, а во-вторых, определить характер смены динамических режимов, а следовательно и функциональных состояний, им соответствующих.

Составляющие компоненты микроструктурной модели паттерна вариабельности ритма сердца (HRV) включают вектор из повторяющихся значений предыдущего и последующего межпульсовых интервалов, а, следовательно, временную составляющую из нулевых, укорачивающих и удлиняющих коррекций межпульсовых интервалов. Алфавит системы всегда постоянен и состоит из фиксированных классов дифференциальной гистограммы распределения паттерна HRV, включающих норму, тахи- и брадиритмию.

Данная модель рассматривается в виде последовательного развертывания цепи событий, имеющих условно-вероятностный характер. Вычисления производятся по основной выборке в 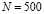кардиоинтервалов: всю полученную шкалу длительностей межпульсовых интервалов делят на классовые интервалы по 0,05 секунды. По выборке кардиоинтервалов строят дифференциальную кривую распределения и вычисляют значение фактической энтропии.

Каждая пара межпульсовых интервалов определяет временную составляющую из нулевых, укорачивающих и удлиняющих коррекций межпульсовых интервалов. Вводится в рассмотрение непрерывная случайная величина X, значения которой связываются с длиной и видом коррекции. Все наблюдаемые значения признака X попадают в интервал (0,22-1,71 секунды), который проходится с шагом в 0,05 секунд.

Таким образом, алфавит системы включает 61 класс дифференциальной гистограммы распределения паттерна вариабельности ритма сердца, а именно: диапазон 30-ти ускоряющих коррекций, диапазон 30-ти замедляющих коррекций и один диапазон нулевых коррекций.

Информационные показатели модели соответствуют параметрам энтропии ритма сердца. Функциональные показатели модели характеризуются формулами вычисления параметров энтропии ритма сердца, каждый из которых характеризует ту или иную меру процесса. Нормированная энтропия 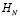отражает степень активности автономной нервной системы [31, 32, 45].

Нормированная энтропия вычисляется по формуле:

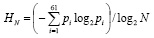. (5)

Отметим, что энтропия системы с конечным множеством состояний достигает максимума, когда все состояния равновероятны.

В результате анализа нормированной энтропии выделяются шесть интервальных классов, которые соответствуют известным функциональным состояниям и дифференцированной степени активности автономной нервной системы человека:

1. РВП СНС (резко выраженное преобладание симпатической нервной системы);

2. ВП СНС (выраженное преобладание симпатической нервной системы);

3. УП СНС (умеренное преобладание симпатической нервной системы);

4. НОРМА (равновесное состояние между симпатикусом и парасимпатикусом);

5. УП ПСНС (умеренное преобладание парасимпатической нервной системы);

6. ВП ПСНС (выраженное преобладание парасимпатической нервной системы).

В задачах диагностики функциональных состояний человека в режиме on-line целесообразно использовать интеллектуальные системы, учитывающие контекстную информацию. При реализации такого рода систем также необходима непрерывная обработка большого потока электрофизиологической информации. Высокая производительность интеллектуальных систем обработки электрофизиологической информации может быть достигнута за счет выполнения интеллектуальных ядер в виде нейросетевых модулей [41, 64].

В работе [67] описано решение задачи автоматического распознавания степени активности автономной нервной системы (АНС) у здоровых лиц, находящихся в различных функциональных состояниях на основе моделирования двухслойной прямонаправленной искусственной нейронной сети (61 – 10 – 6).

При формировании целевых выходных векторов 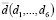, предназначенных для обучения искусственной нейронной сети, эксперт учитывал значение нормированной энтропии. Позиция правильного выходного класса маркировалась в целевом векторе значением 0,5. Остальные координаты целевого вектора принимали значение: – 0,5.

На входы искусственной нейронной сети подавались частоты интервального вариационного ряда, соответствующие реализациям случайной величины Х в алфавите системы.

Координаты входного вектора были равны частотам ранжированной совокупности коррекций ритма сердца, сгруппированных по интервалам: (–1,5; 1,5) ,…, (–0,1; –0,05), (–0,05; 0,05), (0,05; 0,1), …, (1,5; 1,55).

Входы сети 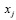, , 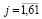были подвергнуты процедуре нормализации вычитанием их выборочного среднего и нормированием на квадратный корень из их исправленной выборочной дисперсии.

Активность нейронов скрытого слоя 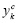, , 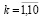вычислялась по формулам:

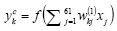, (6)

где 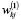– весовой коэффициент связи между j-м входом и k-м нейроном скрытого слоя.

В качестве активационной функции был взят гиперболический тангенс.

Активность нейронов выходного слоя 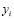, , 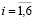вычислялась по формулам:

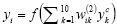, (7)

где 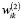– весовой коэффициент связи между k-м нейроном скрытого слоя и i-м нейроном выходного слоя.

Номер нейрона выходного слоя, имеющего максимальную активность, служит маркером класса, к которому сеть относит входной пример.

Искусственная нейронная сеть обучается по алгоритму обратного распространения ошибки, включающему следующие этапы:

1. Инициализация сети со случайными значениями весовых коэффициентов. При инициализации сети все весовые коэффициенты принимают случайные значения из отрезка .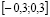

2. Вычисление текущих выходных сигналов для случайно выбранного из обучающей выборки входного вектора.

3. Выполнение настройки синаптических весов.

Коррекции весовых коэффициентов связи осуществляются в направлении антиградиента целевой функции, определяемой формулой:

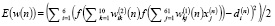, (8)

где 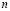– дискретное время;

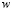– матрица весовых коэффициентов связи;

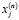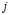– -я координата входного вектора, поданного в момент времени ;

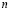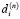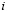– -я координата соответствующего целевого вектора, сформированного врачом-экспертом;

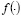– функция активации нейронов скрытого и выходного слоев.

Корректировка синаптических коэффициентов связи выполнялась по формулам:

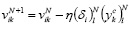, (9)

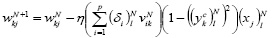, (10)

где 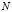– дискретный момент времени, 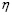– скорость обучения, .

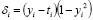4. Шаги 2?3 повторяются до тех пор, пока не будет достигнут приемлемый уровень ошибок I и II-го рода на обучающей выборке.

При работе сети в режиме функционирования отклик сети на входной вектор определяется по формулам:

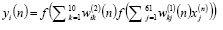, (11)

где .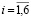

Распознавание класса происходит по максимальному уровню выходного сигнала нейрона, связанного при обучении с одним из шести классов: РВП СНС, ВП СНС, УП СНС, Норма, УП ПСНС, ВП ПСНСП.

В работе [49] были проведены исследования на адекватность описанных нейросетевых моделей реальным электрофизиологическим процессам. Для этого были проанализированы 189 записей межпульсовых интервалов у 94 практически здоровых студентов Белгородского государственного университета. Все обследуемые входили в одну социальную и возрастную группу от 17 до 24 лет.

Обучающая выборка включала 139 записей у 69 человек. В экзаменационную выборку входили 25 человек, у которых были проанализированы 50 записей межпульсовых интервалов.

Нейросетевой алгоритм на обучающей выборке правильно отобрал 94,0% больных. Неправильно распознано – 4,0%. Из них гиподиагностика составила всего 4,0%, случаев гипердиагностики алгоритм не допустил. Чувствительность алгоритма распознавания составила 100,0% (70,0/70,0 + 0,0), специфичность дифференциальной диагностики – 86,7% (26,0/26,0 + 4,0).

Нейросетевой алгоритм на экзаменационной выборке правильно отобрал 93,0% больных. Неправильно распознано – 7,0%. Из них гипердиагностика составила 5,0% и гиподиагностика 2,0%.

Чувствительность алгоритма распознавания составила 97,1% (68,0/68,0 + 2,0), специфичность дифференциальной диагностики – 83,3% (25,0/25,0 + 5,0).

Ошибки классификации составили 7%, что существенно ниже ошибок распознавания, допускаемых врачом. Нейросетевой алгоритм завысил класс степени активности АНС только в 5% случаев, а занизил всего лишь в 2% случаев.

Полученные результаты можно улучшить, устранив недостатки алгоритма обратного распространения ошибки [17, 18, 81, 86], к которым можно отнести: «застревание» процесса обучения в локальных минимумах функции ошибки и переобучение сети за счет включения стохастической составляющей.

Так в работах [51, 69] для обучения сети, решающей задачу автоматической диагностики функциональных состояний человека, была использована комбинация градиентного и стохастического метода обучения Коши.

В процессе обучения пошаговая корректировка весов выполнялась не только в направлении оценки антиградиента целевой функции, но и включала стохастическую компоненту. Перерасчет весов проводился по формулам:

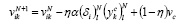, (12)

×

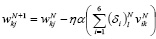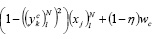×, (13)

где 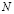– дискретный момент времени, 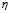– коэффициент, управляющий относительными величинами градиентной и стохастической компонент веса, 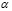– скорость обучения, 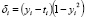, 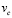и 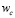– стохастические изменения соответствующих весов.

После корректировки весовых коэффициентов рассчитывалось значение целевой функции. Если в процессе корректировки весовых коэффициентов ошибка сети уменьшалась, то изменения весов сохранялись. В противном случае новые веса сохранялись с “вероятностью”, определяемой распределением Коши:

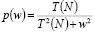, (14)

где 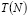– искусственная температура, рассматриваемая как функция времени:

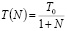, (15)

где 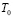– начальная искусственная температура.

Стохастические компоненты коррекции весового коэффициента определялись формулой:

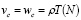tg(P(w), (16)

где 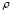– скорость обучения, 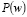– “вероятность” изменения веса на величину .

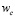В качестве 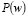выбиралось случайное число из равномерного распределения на интервале 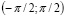. Отрицательная часть введена в рассмотрение для случайного определения знака коррекции.

В среднем после 1000 обучающих эпох сеть устойчиво выходила на 100% уровень верной классификации на обучающей выборке, допуская при этом 2% ошибок первого рода на контрольной выборке [71].

Добавление стохастической составляющей позволило построить систему, которая сходится быстрее, гарантируя при этом нахождение глобального минимума, и не допускает насыщения сетевых нейронов, приводящего к “параличу” сети.

Выводы

1. Проблема своевременной и правильной диагностики тяжелых нарушений ритма сердца и прогнозирования их исходов относится к актуальным задачам кардиологии. Разработка информационных систем с базами знаний позволит повысить качество медицинской помощи населению. Особенно ценным и актуальным является системный подход к проблеме принятия диагностических решений и разработке на его основе общедоступных сервисов для самодиагностики и текущего контроля собственного состояния пациента. В настоящее время технические и программные средства дают качественно новые возможности обработки медицинских данных.

2. Существует ряд проблем, специфичных для задач медицинской диагностики, затрудняющих применение объективных математических методов. Во многих задачах медицинской диагностики не всегда удается выделить перечень классов, которые удовлетворяли бы требованиям полноты и непересекаемости.

3. Разработка алгоритмов и программ для моделирования нормальной сердечной деятельности и различных нарушений ритма и проводимости является весьма перспективной задачей, поскольку математическое моделирование позволяет раскрыть новые черты патогенеза некоторых нарушений ритма и проводимости.

4. Алгоритмы автоматической классификации ритма сердца различаются по характеру и числу используемых электрокардиографических признаков, числу диагностируемых классов и виду, решающих правил, большая часть которых представлена пороговыми алгоритмами. Ряд авторов считает, что для практического использования в системах кардиологического контроля необходимо применение более сложных алгоритмов, обладающих способностью к адаптации и к учёту контекста электрокардиосигнала. В частотности, распознавание мерцательной аритмии целесообразно проводить с использованием оценок энтропии Колмогорова.

5. Для целей классификации нарушений синусового ритма применяются методы условно-вероятностного анализа, корреляционной ритмографии, скаттерографии, нелинейной динамики, спектрального анализа. Известны геометрические алгоритмы дифференциации авторегрессионных облаков у больных с синдромом фибрилляции предсердий, базирующиеся на поиске сгущения точек в заданной экспертом зоне. Более надежными и близкими к врачебной логике распознавания являются алгоритмы, основанные на использовании элементов теории нечетких множеств и искусственных нейронных сетей.

6. Метод корреляционной ритмографии позволяет разделить больных с синдромом фибрилляции предсердий на несколько функциональных классов в зависимости от типа авторегрессионного облака (АРО):

1. Мономодальный симметричный,

2. Мономодальный асимметричный,

3. Мономодальный инвертированный,

4. Полимодальный,

5. Амодальный.

Мономодальные типы АРО являются прогностически благоприятными и свидетельствует о вполне удовлетворительном функциональном состоянии сердца. В случае полимодального и амодального классов АРО перспективы на восстановление и удержание правильного синусового ритма сомнительны.

7. К методам автоматической диагностики, обладающим способностью к адаптации и к учёту контекста электрокардиосигнала, прежде всего, относят методы нейрокомпьютинга. Единицей обработки информации в них выступает искусственный нейрон, в состав которого входят синаптические веса, сумматор и функция активации. Используются такие функции активации, как пороговая, кусочно-линейная, сигмоидальная и гиперболический тангенс. Искусственную нейронную сеть можно представить в виде направленного графа, состоящего из узлов, соединенных синаптическими и активационными связями. Основными архитектурами искусственных нейронных сетей являются однослойные и многослойные сети прямого распространения, а также рекуррентные сети. Целью процесса обучения сети является вычисление значений синаптических весов.

8. Существуют методы автоматического прогнозирования исходов мерцательной аритмии, основанные на моделировании однослойных и многослойных нейронных сетей. Известен также метод автоматической диагностики функциональных состояний человека, основанный на моделировании двухслойной прямонаправленной искусственной нейронной сети, обученной по алгоритму обратного распространения ошибки.

10. Алгоритм обратного распространения ошибки имеет ряд недостатков, к которым относят «застревание» процесса обучения в локальных минимумах функции ошибки и переобучения сети за счет включения стохастической составляющей. Оптимизация обучения сети осуществляется посредством комбинации градиентного и стохастического методов обучения. Гибридная система сходится быстрее, гарантируя при этом нахождение глобального минимума, и не допуская насыщения сетевых нейронов, приводящего к “параличу” сети.

11. Анализ литературы показывает, что искусственные нейронные сети дают гибкий инструментарий в автоматическом распознавании функциональных состояний человека и некоторых нарушений ритма сердца, который точно можно настроить под мнение авторитетного эксперта. Обученные нейросетевые системы обладают способностью к адаптации и к учёту контекста кардиосигнала, оказываются более выигрышными в плане временных затрат на обработку эмпирических данных, обеспечивая при этом такие полезные свойства систем, как адаптивность, масштабируемость, отказо- и помехоустойчивость.